Scatter plots with lots of points
Overlapping
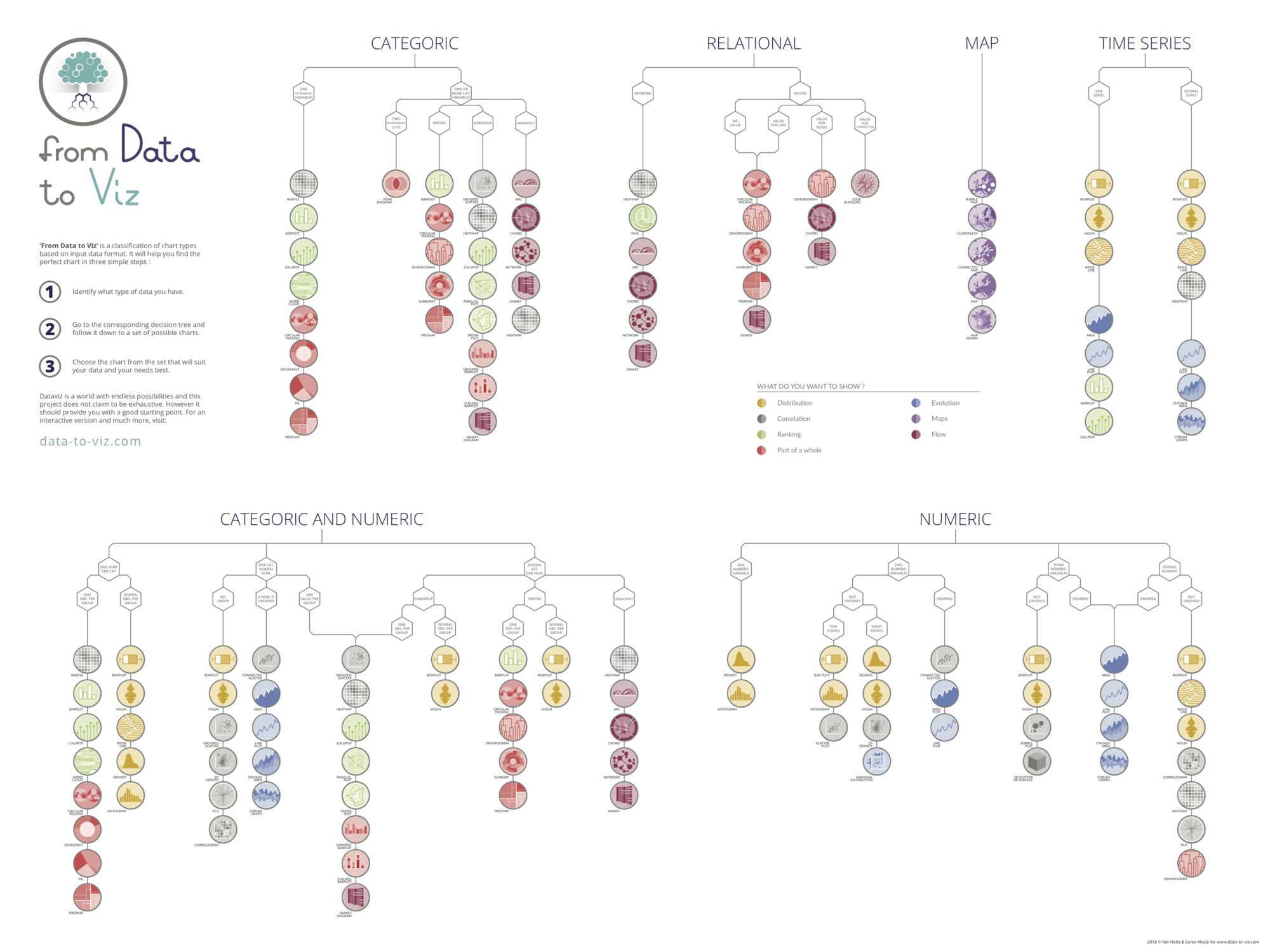
Consider the scatterplot on the left hand side of this figure. A lot of dots overlap and they make the figure hard to read. Even worse, it is impossible to determine how many data points are in each position.
In this case, a possible solution is to cut the plotting window into several bins, and represent the number of data points in each bin by a color. Following the shape of the bin, this makes Hexbin plot or 2D histogram.
KDE plots
Then, it is possible to make a smoother result using Gaussian KDE (kernel density estimate). Its representation is called a 2D density plot, and you can add a contour to denote each step. You can see more examples of these types of graphics in the 2D density section of the Gallery.
# Libraries
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde
# Create data: 200 points
data = np.random.multivariate_normal([0, 0], [[1, 0.5], [0.5, 3]], 200)
x, y = data.T
# Create a figure with 6 plot areas
fig, axes = plt.subplots(ncols=7, nrows=1, figsize=(25, 5))
# Everything starts with a Scatterplot
axes[0].set_title('Scatterplot')
axes[0].plot(x, y, 'ko')
# As you can see there is a lot of overlapping here!
# Everything starts with a Scatterplot
axes[1].set_title('Scatterplot')
axes[1].scatter(x, y, color='green', edgecolor='black')
# Thus we can cut the plotting window in several hexbins
nbins = 20
axes[2].set_title('Hexbin')
axes[2].hexbin(x, y, gridsize=nbins, cmap=plt.cm.BuGn_r)
# 2D Histogram
axes[3].set_title('2D Histogram')
axes[3].hist2d(x, y, bins=nbins, cmap=plt.cm.BuGn_r)
# Evaluate a gaussian kde on a regular grid of nbins x nbins over data extents
k = gaussian_kde(data.T)
xi, yi = np.mgrid[x.min():x.max():nbins*1j, y.min():y.max():nbins*1j]
zi = k(np.vstack([xi.flatten(), yi.flatten()]))
# plot a density
axes[4].set_title('Calculate Gaussian KDE')
axes[4].pcolormesh(xi, yi, zi.reshape(xi.shape), shading='auto', cmap=plt.cm.BuGn_r)
# add shading
axes[5].set_title('2D Density with shading')
axes[5].pcolormesh(xi, yi, zi.reshape(xi.shape), shading='gouraud', cmap=plt.cm.BuGn_r)
# contour
axes[6].set_title('Contour')
axes[6].pcolormesh(xi, yi, zi.reshape(xi.shape), shading='gouraud', cmap=plt.cm.BuGn_r)
axes[6].contour(xi, yi, zi.reshape(xi.shape) )
plt.show()Going further
You might be interested in:
- create contour plots
- create 2d histograms
- create hexbin plots